在数学领域中,函数是描述变量之间关系的重要工具。根据函数的性质,我们可以将它们分为奇函数、偶函数和其他类型的函数。奇函数和偶函数因其独特的对称性而备受关注。本文将深入探讨一个有趣的问题:奇函数乘以偶函数等于什么?
一、奇函数与偶函数的定义
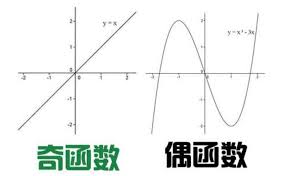
首先,我们需要明确奇函数和偶函数的定义:
- 奇函数:如果对于函数$f(x)$,有$f(-x) = -f(x)$对所有在其定义域内的$x$都成立,那么$f(x)$是奇函数。例如,$f(x) = x^3$就是奇函数。
- 偶函数:如果对于函数$g(x)$,有$g(-x) = g(x)$对所有在其定义域内的$x$都成立,那么$g(x)$是偶函数。例如,$g(x) = x^2$就是偶函数。
二、奇函数与偶函数的性质
奇函数和偶函数具有一些显著的数学性质,这些性质在解题时非常有用:
- 奇函数的图像关于原点对称:即,图像在$x$轴上方和下方的部分是关于原点对称的。
- 偶函数的图像关于$y$轴对称:即,图像在$y$轴的左侧和右侧的部分是关于$y$轴对称的。
- 奇函数在$x=0$处的值为0(如果0在其定义域内):这是因为$f(0) = -f(0)$,唯一满足这一条件的数是0。
- 偶函数在$x=0$处的值可能是任意实数:因为$g(0) = g(0)$,不产生矛盾。
三、奇函数乘以偶函数的结果
现在,我们来分析奇函数乘以偶函数的结果。设$h(x) = f(x) ⁄⁄cdot g(x)$,其中$f(x)$是奇函数,$g(x)$是偶函数。
1. 对称性分析:
- 由于$f(x)$是奇函数,其图像关于原点对称。
- 由于$g(x)$是偶函数,其图像关于$y$轴对称。
- 当我们将两者相乘时,由于奇函数和偶函数的对称性,$h(x)$的图像将不再具有关于原点或$y$轴的对称性。
2. 奇偶性分析:
- $h(-x) = f(-x) ⁄⁄cdot g(-x)$
- 由于$f(-x) = -f(x)$且$g(-x) = g(x)$,代入上式得:

$h(-x) = -f(x) ⁄⁄cdot g(x) = -h(x)$
- 这表明,$h(x)$既不是奇函数(因为$h(-x) ⁄⁄neq h(x)$),也不是偶函数(因为$h(-x) ⁄⁄neq -h(x)$)。我们称这样的函数为非奇非偶函数。
3. 具体例子:
- 设$f(x) = x$(奇函数)和$g(x) = x^2$(偶函数)。
- 则$h(x) = f(x) ⁄⁄cdot g(x) = x ⁄⁄cdot x^2 = x^3$。
- 但这里需要注意,虽然$h(x) = x^3$看起来像一个奇函数,这是因为我们选择的$f(x)$和$g(x)$恰好使得$h(x)$的形式保持为奇函数。在一般情况下,奇函数乘以偶函数的结果将是一个非奇非偶函数。
四、结论
综上所述,奇函数乘以偶函数的结果是一个非奇非偶函数。这一结论基于奇函数和偶函数的定义及其对称性质。通过具体的例子,我们可以进一步验证这一结论。在数学学习和研究中,了解不同类型的函数及其性质对于解决问题至关重要。希望本文能帮助读者更好地理解和应用奇函数和偶函数的概念。